Gamma函数是一个在数学分析中非常重要的函数，通常表示为Γ，其中n是实数或复数。Gamma函数可以看作是阶乘函数的推广，它在许多数学领域都有应用，比如概率论、统计学、物理学和工程学等。

Gamma函数的定义是：

Γ = ∫ x^e^ dx

对于正整数n，Gamma函数的值等于n1的阶乘，即Γ = !。但对于非整数值，Gamma函数的值需要通过积分来计算。

Gamma函数表通常列出了Gamma函数在特定点的值。这些值可以是近似值，也可以是精确值，取决于计算方法。以下是一些常见的Gamma函数表中的值：

n | Γ

1 | 1

2 | 1

3 | 2

4 | 3

5 | 4

6 | 5

7 | 6

8 | 7

9 | 8

10 | 9

这些值都是精确值，因为它们对应于整数n的阶乘。对于非整数值，Gamma函数的值需要通过数值积分或查表来获得。在实际应用中，通常使用计算机软件或计算器来计算Gamma函数的值。探索gamma函数表的奥秘：数学世界的璀璨明珠

亲爱的读者们，你是否曾在数学的海洋中迷失方向，对那些看似复杂无趣的公式感到困惑？今天，就让我们一起揭开gamma函数表的神秘面纱，探寻数学世界的璀璨明珠。

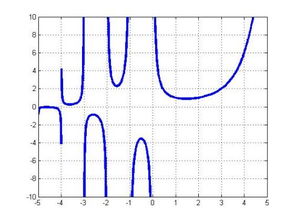
一、gamma函数的诞生

在数学的殿堂里，有一个特殊的函数，它既不是初等函数，也不是常见的三角函数，却拥有着广泛的应用。这个函数就是gamma函数，也被称为伽马函数。

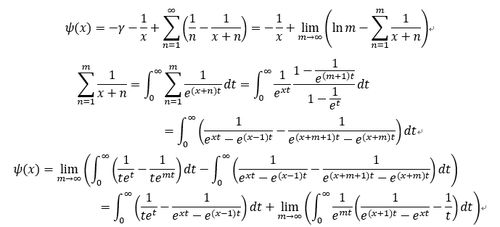
gamma函数的诞生要追溯到18世纪，当时数学家们正致力于将阶乘的概念从整数领域扩展到实数领域。经过一番努力，数学家们终于找到了这个神奇的函数，它不仅填补了阶乘的空缺，还在数学的各个领域大放异彩。

二、gamma函数的定义

gamma函数的定义如下：

\\[ \\Gamma(z) = \\int_0^\\infty t^{z-1} e^{-t} dt \\]

其中，\\( z \\) 是一个复数，且 \\( \\text{Re}(z) > 0 \\)。这个公式看似复杂，实则蕴含着丰富的数学内涵。

三、gamma函数的性质

gamma函数具有许多有趣的性质，以下列举几个：

1. 递推关系：\\( \\Gamma(z 1) = z\\Gamma(z) \\)

2. 基本值：\\( \\Gamma(1) = 1 \\)，\\( \\Gamma\\left(\\frac{1}{2}\\right) = \\sqrt{\\pi} \\)

3. 阶乘的推广：对于正整数 \\( n \\)，有 \\( \\Gamma(n 1) = n! \\)

4. 复数域上的定义：gamma函数在整个复平面上都有定义

四、gamma函数的应用

gamma函数在数学、物理学、工程学等领域都有着广泛的应用，以下列举几个例子：

1. 概率论与统计学：gamma函数在概率论中有着重要的地位，如伽马分布、贝塔分布等都与gamma函数密切相关。

2. 物理学：在物理学中，gamma函数可以用来描述粒子的能量和动量等特性。

3. 工程学：在工程学中，gamma函数可以用于信号处理、图像处理等领域。

五、gamma函数表

为了方便查阅gamma函数的值，人们编制了gamma函数表。gamma函数表通常包含以下内容：

1. gamma函数的值：列出不同 \\( z \\) 值对应的gamma函数值。

2. gamma函数的性质：介绍gamma函数的递推关系、基本值等性质。

3. gamma函数的应用：列举gamma函数在各个领域的应用实例。

gamma函数表是数学研究和工程实践的重要工具，它可以帮助我们快速找到gamma函数的值，从而解决实际问题。

gamma函数是数学世界中的一颗璀璨明珠，它不仅填补了阶乘的空缺，还在各个领域发挥着重要作用。通过本文的介绍，相信你对gamma函数有了更深入的了解。在今后的学习和工作中，不妨多关注gamma函数，相信它会给你带来意想不到的收获。

未经允许不得转载：91黑料网 » gamma函数表,伽马函数表解析与应用概览